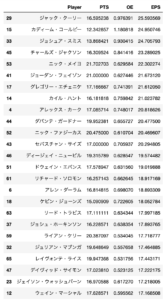
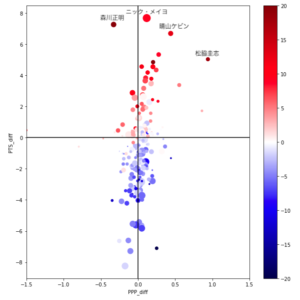
正規分布を使って千葉ジェッツの勝ち試合数をシミュレーションしました

Dean Oliver著『Basketball on Paper』（以下BoP）を読み進めているらんそうるいです。BoPの11章『Basketball’s Bell Curve』に、得点の平均・標準偏差、失点の平均・標準偏差、得点と失点の相関を指定した2つの正規分布の乱数（得点・失点を表す）によって、そのシーズンの勝ち試合数をかなりの精度で予測できるという記述がありました。

　この記事では、この正規分布を使ったシミュレーションをBリーグ2020-21シーズンの千葉ジェッツのデータを用いて行い、勝ち試合数を予測してみたいと思います。結果を先に書くと、勝ち試合数の予測は実際の勝ち試合数よりも1勝分だけ少なく見積もるというもので、このシミュレーションの精度はかなり良いのではないか、と考えられました。

データセット

Bリーグ2020-21シーズンのボックススコアを公開されているrintaromasuda様（https://github.com/rintaromasuda/bleaguer/tree/master/inst/extdata）のデータを用いました。使用したデータは「games_summary_202021.csv」と「teams.csv」です。これらのデータを連結してデータセットとしました。

方法

まず、千葉ジェッツの試合をデータセットから抽出しました。その後、ScheduleKeyを基に対戦相手のデータをデータセットから抽出しました。この操作によって、千葉ジェッツとその対戦相手の得点が記録されたデータセットが作成できました。

　こうして得られたデータセットから、千葉ジェッツの得点の平均・分散、対戦相手の得点（つまり千葉ジェッツの失点）の平均・分散を計算しました。さらに、千葉ジェッツの得点・対戦相手の得点の共分散を計算しました。

　最後に、Pythonのnumpy.random.multivariate_normal()関数に、平均・分散共分散行列・試合数を渡して、千葉ジェッツの得点を表す正規分布・対戦相手の得点を表す正規分布から、得点・失点を表す乱数を42組生成しました。ただし、この乱数は相関（r=0.294）を持っていることに注意してください。生成した乱数の組の大小を比較し、得点を表す乱数のほうが失点を表す乱数よりも大きかった場合は、勝ち試合とみなして、勝ち試合数を数えました。

結果

まず、千葉ジェッツの実際の勝ち試合数は42試合中32勝でした。得失点のヒストグラムは下図のようになりました。得点の平均は88.238、分散は207.210です。失点の平均は77.881、分散は183.766です。得点と失点の共分散は57.322です。

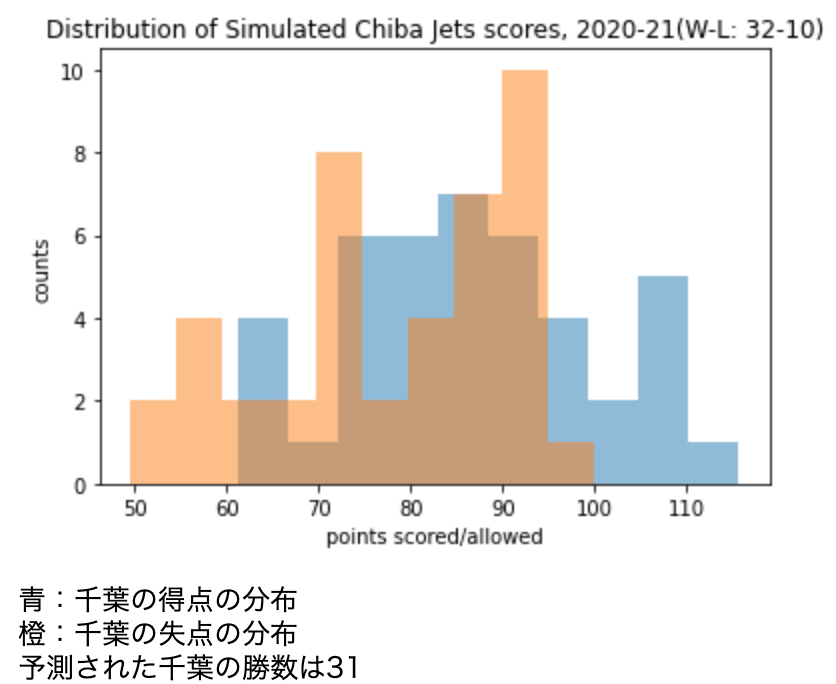
　シミュレーションで得られた千葉の得失点のヒストグラムは下図のようになりました。シミュレーションにあたって、平均・分散共分散行列は実際のデータで得られた値を指定しました。42組の得失点の大小を比較して勝ち試合数を計算したところ、31勝という結果が得られました。かなり精度の良い予測になっていると言えるのではないでしょうか？

終わりに

この記事ではBoPで紹介されていた、得失点の正規分布を用いたシーズンの勝ち試合数の予測をしてみました。その結果、かなり精度の良い予測結果が得られました。2021-22シーズンが開幕してしばらく経ってから、各チームのデータを使って、レギュラーシーズンの勝ち試合数の予測をやってみたいなと思いました。

参考文献

Dean Oliver(2004) Basketball on Paper Rules and Tools for Performance Analysis.

分析に用いたコード（Python）

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

#データの読み込み
data=pd.read_csv("games_summary_202021.csv",encoding="UTF-8")
teams=pd.read_csv("teams.csv",encoding="UTF-8")

#データの抽出（千葉と対戦相手の得点を抽出）
teams=teams[teams["Season"]=="2020-21"]
data=data.merge(teams,on="TeamId")
chiba=data[data["NameShort"]=="千葉"]

chiba_opps=pd.DataFrame(columns=["ScheduleKey","PTS","NameShort","TeamId"])
for key in chiba["ScheduleKey"]:
    chiba_opps=chiba_opps.append(data[data["ScheduleKey"]==key].loc[:,["ScheduleKey","PTS","NameShort","TeamId"]])

#ScheduleKeyでソートする
opps=chiba_opps[chiba_opps["NameShort"]!="千葉"].sort_values("ScheduleKey")
chiba=chiba_opps[chiba_opps["NameShort"]=="千葉"].sort_values("ScheduleKey")

#千葉の得点の平均と分散を出す
chiba["PTS"].mean()#88.238
chiba["PTS"].var()#207.210

#対戦相手の平均とSDを出す
opps["PTS"].mean()#77.881
opps["PTS"].var()#183.766

#千葉ジェッツの得点・失点のヒストグラムを書く
plt.hist(chiba["PTS"],alpha=0.5)
plt.hist(opps["PTS"],alpha=0.5)
plt.title("Distribution of Chiba Jets scores, 2020-21(W-L: 32-10)")
plt.xlabel("points scored/allowed")
plt.ylabel("counts")
plt.show()
print("青：千葉の得点の分布\n橙：千葉の失点の分布\n千葉の勝数は32")

chiba=chiba.reset_index()
opps=opps.reset_index()

#分散共分散行列の算出
c_pts=[]
o_pts=[]
for pts_c,pts_o in zip(chiba["PTS"],opps["PTS"]):
    c_pts.append(pts_c)
    o_pts.append(pts_o)
np.cov(c_pts,o_pts)#57.322

#相関係数の算出
np.corrcoef(c_pts,o_pts)

#正規分布から乱数を生成する
np.random.seed(20210419)
mean=[88.238,77.881]
cov=[[207.210,57.322],[57.322,183.766]]
score=np.random.multivariate_normal(mean,cov,42)#このデータセットの千葉の試合数は42
score=pd.DataFrame(score).set_axis(["point_scored","point_allowed"],axis=1)

#ヒストグラムを書く
plt.hist(score["point_scored"],alpha=0.5)
plt.hist(score["point_allowed"],alpha=0.5)
plt.title("Distribution of Simulated Chiba Jets scores, 2020-21(W-L: 32-10)")
plt.xlabel("points scored/allowed")
plt.ylabel("counts")
plt.show()
print("青：千葉の得点の分布\n橙：千葉の失点の分布\n予測された千葉の勝数は31")

#勝数の予測値を算出する
win=0
for scored,allowed in zip(score["point_scored"],score["point_allowed"]):
    if scored>allowed:#勝ったとき
        win=win+1
        
print("予測される千葉の勝数は",win)

#実際の勝数を算出する
win=0
for scored,allowed in zip(chiba["PTS"],opps["PTS"]):
    if scored>allowed:
        win=win+1

print("実際の千葉の勝数は",win)