1-year RAPMはどれくらい信用できるのか?
サマリー
- B League B1 2022-23, 2023-24シーズンのデータをランダムに分割して、擬似的に1-year RAPMを2つ作成し、これらの関係を調査した。
- もし、1-year RAPMが選手の貢献度を定量化することができており、さらにランダムに分割した2つのデータセットの間でデータの挙動が同じであるとしたら、2つの1-year RAPMは全く同じ値を取ることが期待できる。
- 擬似的に作成された1-year RAPM同士の相関係数は大きくはなく(r=0.50程度)、MAEは大きかった(-10 ~ 10の範囲を取るデータに対して2.5程度の誤差が生じていた)。
- これらの結果から、1-year RAPMは信用できないことがわかった。また、POSSの回数が多くなるにつれて、RAPMの値の信頼性が向上していくという結果も観察できなかった。
RAPMとは?
RAPM (Regularized Adjusted Plus-Minus) とは、選手の出場情報と得点の推移から計算されるオールインワンメトリクスの一つである。オールインワンメトリクスとは、バスケットボール選手の貢献を一つの値で定量化したデータである。
RAPMは2010年にSillによって提案され、様々なオールインワンメトリクスが開発される契機となった。たとえば、BPM (Box Plus-Minus) はボックススコアから、RAPMと近い評価値を得ることを目指したオールインワンメトリクスである。このように、RAPMは他のオールインワンメトリクスの「親」ないしは「教師」のような存在であり、特別なデータとして重宝されてきた。
RAPMによる貢献度の定量化には数シーズン分のデータが必要であると、バスケットボールのデータ分析コミュニティでは了解されており、1シーズンのデータによるRAPMはあまり信頼できないと考えられていた 。しかし、1シーズンのデータから計算したRAPMがどの程度信用できないのか、あるいは意外と信用できるものなのかを検討した調査は公表されていないように思う。
そこで、1-year RAPMがどの程度一貫した値を返すのか (この程度を「信頼性」と呼ぼう)、そして、データが集まりさえすれば信頼性は向上していくのかを、この調査では検討した。
調査内容
データの取得
Bリーグ公式HPから、B1 2022-23, 2023-24シーズンのデータを取得した。各シーズンとも60 x 24 / 2で720試合分のデータを使った調査が理想ではあるが、スクレイピングの失敗や情報の不備などで、各シーズンとも20試合程度のデータを分析に使うことができなかった。しかし、今回の調査の目的は正確に選手の貢献度を定量化することではなく、RAPMの挙動を調べることであったため、データが完全でなくても大きな問題にはならないと判断し、データ分析を行なった。
調査の手法
2022-23シーズンと2023-24シーズンのデータを一度まとめた後、ランダムにデータを2分割して、擬似的に1-year RAPMを2つ作成して、それらの関係を調査した。
直感的には、2022-23シーズンと2023-24シーズンのデータを別々に用いて、1-year RAPMを2つ作成してシーズンの間で関係を調べることが定石であるが、敢えてそうしなかった理由を説明する。
RAPMという手法を純粋に評価するには、なるべくRAPMの責任ではない要因によって、RAPMの挙動が影響を受けることを避けるべきだと考えた。そうした要因としては、たとえば選手自身が移籍してしまうことや、選手自身は移籍していなかったとしてもチーム内での役割が変わってしまうことが想像できた。これらの影響を軽減するために、2年分データをランダムに2分割してそれぞれを1年分のデータに見立てる方法を採用した。
結果
2シーズン分のデータをランダムに分割し、得られたデータセットそれぞれからRAPMを計算し、これらを擬似的に1-year RAPMと見なして、これらの関係を調査した。まず、擬似的な1-year RAPMを縦横軸に取り、散布図を描いた。それが下図である。

マーカは選手一人一人を表している。マーカの大きさはその選手が出場したポゼッションが多いほど大きい。対角線には点線が描画されており、擬似的な1-year RAPM同士が全く同じ値を取るとしたら、対角線上にマーカが配置される。この意味で対角線は信頼性が最大の状態を描画したものである。この散布図を観察することで分かることは、対角線上に全てのマーカが配置されるような信頼性が最大の結果には程遠いということである。また、マーカが大きいからと言って、必ずしも対角線上にマーカが配置されているわけではないことも読み取ることができる。これは、POSSが増えてもRAPMの信頼性はほとんど変わらないか、緩やかにしか向上しないことが推測できる。
POSSが多いほどRAPMの信頼性は向上するだろうか? これを直接検討したのが、下図である。この折れ線グラフの縦軸は相関係数である。相関係数とは、2つの数値 (ここではRAPM) の線形な関係の強さを定量化したものであり-1 ~ 1の値を取る。関係が最も弱いのが0であり、絶対値が1に近づくほど関係が強い。横軸は、POSSであり、たとえば、POSS=1000では、分割したデータセットにおける2つのPOSSがいずれも1000以上の選手だけで相関係数を算出したことを意味している。
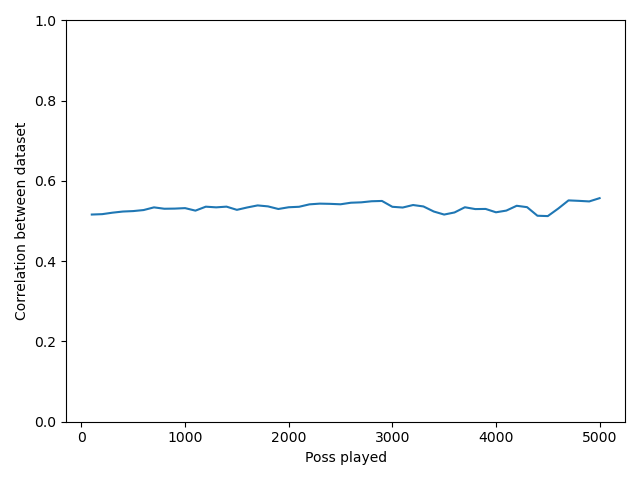
この折れ線グラフから読み取ることができるのは、たとえPOSSが多くなったとしても、相関係数はほとんど変化しないということである。
同様の手続きで平均絶対誤差 (MAE)とPOSSの関係を示したのが下図である。MAEとは『「二つの値の差」の絶対値』の平均値である。B1リーグにおけるRAPMは-10 ~ 10の範囲に収まるケースが多いので、±2.5程度のズレは無視できないくらい大きいと言える。また、やはりPOSSが増えたとしてもMAEは緩やかにしか減少しないことが推測できる。
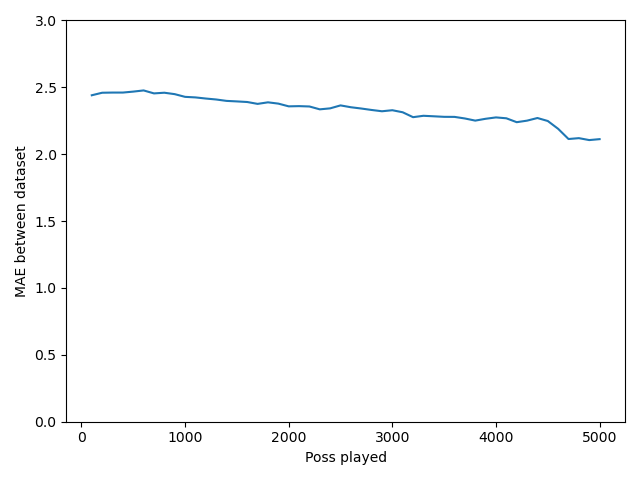
以上の結果をまとめると、擬似的な1-year RAPMの信頼性は、相関係数・MAEいずれの観点でも高くないことがわかった。
